Comme nous l’avons vu, la thermodynamique du 19ème siècle décrit essentiellement les propriétés des systèmes isolés dits fermés. Or ceux-ci n’existent pratiquement pas dans la nature. La notion de système fermé est une idéalisation théorique commode pour le raisonnement, car elle conduit à des propriétés simples et faciles à étudier, mais elle décrit mal les phénomènes réels. Un système fermé atteint rapidement l’équilibre thermodynamique et s’arrête d’évoluer. La notion de système fermé a donc peu d’utilité pour les chercheurs intéressés par une évolution continue telle qu’on l’observe dans la nature.

Seuls les systèmes ouverts hors équilibre évoluent sans cesse. C’est le cas des êtres vivants et plus généralement des structures dites dissipatives. Or, il se trouve que l’univers est fait essentiellement de structures dissipatives. On ne s’en aperçoit pas nécessairement car leur évolution peut être très lente. C’est le cas par exemple des étoiles qui cependant naissent et meurent comme nous. Bien plus, les étoiles sont organisées en galaxies (a) qui elles-mêmes sont organisées en amas de galaxies (b) organisés à leur tour en superamas (c).

On observe ainsi des cascades de structures dissipatives en interaction les unes avec les autres, chaque étage de la cascade redistribuant l’énergie vers d’autres étages. Un système ouvert, formé de structures dissipatives en interaction, étant lui-même une structure dissipative, ce système va automatiquement s’auto-organiser de façon à maximiser la dissipation d’énergie.

Un exemple bien connu d’une telle cascade est la cascade de tourbillons d’un écoulement turbulent. Lorsqu’on augmente la vitesse d’un écoulement turbulent, les tourbillons deviennent instables et se divisent en tourbillons plus petits qui se subdivisent eux-mêmes en tourbillons encore plus petits. L’énergie des gros tourbillons est ainsi transférée à des tourbillons de plus en plus petits jusqu’à sa dissipation finale en chaleur à l’échelle des molécules individuelles.

Une telle cascade de tourbillons porte le nom de cascade de Kolmogorov, du nom du chercheur russe André Kolmogorov (d) qui en a découvert les propriétés. Lorsque le même phénomène physique est responsable du transfert de l’énergie à chaque étage de la cascade, alors les propriétés de la cascade sont les mêmes quelque soit l’étage considéré. On dit que ses propriétés sont invariantes par changement d’échelle. Par exemple l’énergie contenue dans un tourbillon et la taille du tourbillon sont toujours dans la même rapport. Les mathématiciens traduisent cela en disant que la relation entre l’énergie et la taille du tourbillon est une loi de puissance. Cela veut dire que l’énergie d’un tourbillon est proportionnelle à sa taille élevée à une certaine puissance (entière ou fractionnaire). Dans le cas des tourbillons cette puissance vaut 5/3.

Ainsi la turbulence a les propriétés d’un objet fractal (e) au sens de Benoit Mandelbrot (f). Ces objets ont la même apparence quelque soit le grandissement avec lequel on le regarde (autosimilarité). C’est parce que l’énergie se dissipe en cascades que de tels objets sont très répandus dans la nature. Jusque là ils avaient été très peu étudiés à cause de leur complexité. Grâce aux ordinateurs on peut maintenant fabriquer mathématiquement des objets fractals et les représenter graphiquement. Ils sont souvent d’une grande beauté (g) car ils ressemblent à des structures naturelles. Les objets fractals sont caractéristiques du processus d’auto-organisation de l’univers, en particulier du monde vivant.

Un exemple particulièrement complexe de structures dissipatives en interaction est un écosystème (h) Un écosystème est en lui-même une structure dissipative. Il reçoit de l’énergie (principalement d’origine solaire) qu’il redistribue sous d’autres formes. Il absorbe de la matière (eau, oxygène, gaz carbonique, minéraux du sol) qu’il redistribue aussi. Comme dans un tourbillon, certains éléments tournent continuellement en rond dans le système: c’est le cas du cycle de l’azote (i). Un écosystème est formé aussi de cascades d’énergie. Les plantes captent directement l’énergie solaire, puis servent de nourriture aux herbivores, qui eux-mêmes servent de nourriture aux carnivores. On peut observer ainsi jusqu’à cinq cascades successives: l’homme mange des truites, qui mangent des grenouilles, qui mangent des sauterelles, qui mangent de l’herbe. De l’énergie est dissipée à chaque étage. Pour maintenir un homme en vie pendant un an il faudrait au moins 300 truites. Ces truites auront dû manger 90 000 grenouilles, qui auront dû manger 27 millions de sauterelles, ayant elles-mêmes dévoré 1 000 tonnes d’herbe (1). Comme les tourbillons de Kolmogorov, les écosystèmes s’auto-organisent de façon à maximiser la dissipation de l’énergie.

Si une structure trop grosse pour dissiper efficacement l’énergie se subdivise en structures plus petites, il arrive aussi souvent que des structures trop petites pour dissiper efficacement l’énergie collaborent entre elles pour mieux dissiper l’énergie. Nous avons vu l’exemple des gènes dans le génome ou des cellules dans notre organisme. Là encore, il y a auto-régulation de la taille des structures de façon à maximiser la dissipation de l’énergie. Ces mêmes lois s’appliquent aux individus dans une entreprise et aux entreprises dans la société. Nous reviendrons longuement sur ce sujet à la fin de ce blog.

Certains biologistes comme John Whitfield (j) ont cherché à mettre en évidence une relation entre le métabolisme (taux de dissipation d’énergie) des êtres vivants et leur taille. Comme dans le cas des tourbillons de Kolmogorov, ils trouvent une loi de puissance. Ainsi le métabolisme des mammifères apparaît proportionnel à la puissance 3/4 de leur masse. La relation est valable depuis la souris jusqu’à l’éléphant qui est 10⁴ fois plus gros. L’origine de cet exposant (3/4) est toujours discutée. Les mammifères dissipant leur énergie sous forme de chaleur, on s’attendrait à ce que leur métabolisme soit proportionnel à leur surface, qui est elle-même proportionnelle à la puissance 2/3 de leur volume (donc de leur masse). Pourquoi un exposant 3/4 au lieu de 2/3 soit une différence de 1/12?

Je me permets d’offrir ici une suggestion. Eric Chaisson (k) a montré que l’efficacité avec laquelle l’énergie se dissipe dans l’univers n’a cessé d’augmenter. Par exemple les animaux dissipent dix fois plus d’énergie par unité de masse que les plantes apparues apparus 1,5 milliards d’années plus tôt. Il est donc vraisemblable que les gros mammifères, apparus 150 millions d’années plus tard que les petits, dissipent un peu plus efficacement l’énergie que ces derniers. Pour rendre compte de la différence entre les deux exposants, il suffit d’un facteur (10⁴)^1/12 ou 10^1/3 c’est-à-dire de l’ordre de 2, ce qui semble compatible avec la courbe de Chaisson (voir figure).

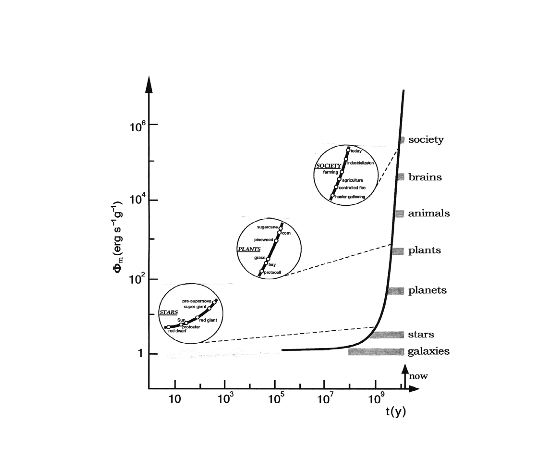
Évolution du taux de dissipation de l’énergie (par unité de masse) en fonction de l’âge de l’univers (d’après Eric Chaisson)

D’après cette courbe, le cerveau humain dissiperait dix fois plus d’énergie par unité de masse qu’un corps animal et dix mille fois plus qu’une étoile. Comme nous avons vu dans notre précédent article (no. 17), un nouvel ordre de grandeur vient encore d’être franchi avec les sociétés humaines. La courbe de Chaisson montre une accélération continuelle de l’évolution. Le taux de dissipation de l’énergie est multiplié par 10 sur des intervalles de temps de plus en plus courts. Il ne s’agit donc pas d’une simple croissance exponentielle. Plus qu’une explosion, c’est une véritable déflagration dont peu de gens ont pris conscience. Et ceux qui en prennent conscience (2, 3) n’en connaissent généralement pas l’origine thermodynamique.

Pour bien comprendre l’évolution, il est nécessaire de passer en revue le processus d’auto-organisation de l’univers depuis le Big Bang. Je me propose de le faire dans le prochain article.

Références:
(1) Eric Chaisson, Cosmic Evolution: the Rise of Complexity in Nature (Harvard Univ. Press, 2002). Voir aussi le site Web: http://www.tufts.edu/as/wright_center/cosmic_evolution/docs/text/text_chem_7.html
(2) Ray Kurzweil, The Singularity is Near: When Humans Transcend Biology (Penguin, 2006).
(3) André Lebeau, L’engrenage de la technique (Gallimard, 2005)

Liens internets:
(a) http://fr.wikipedia.org/wiki/Galaxie
(b) http://fr.wikipedia.org/wiki/Amas_de_galaxies
(c) http://fr.wikipedia.org/wiki/Superamas
(d) http://en.wikipedia.org/wiki/Andrey_Kolmogorov
(e) http://fr.wikipedia.org/wiki/Fractale
(f) http://fr.wikipedia.org/wiki/Benoît_Mandelbrot
(g) http://www.oyonale.com/fractals/gtf31.htm
(h) http://fr.wikipedia.org/wiki/Écosystème
(i) http://fr.wikipedia.org/wiki/Cycle_de_l’azote
(j) http://biology.plosjournals.org/perlserv/?request=get-document&doi =10.1371%2Fjournal.pbio.0020440
(k) http://www.tufts.edu/as/wright_center/eric/reprints/big_history.pdf