Bien qu’abstraite, la notion d’énergie nous est devenue familière grâce à sa production industrielle sous des formes variées: énergie thermique, hydroélectricité, énergie nucléaire, etc… Encore plus abstraite, la notion d’information nous devient elle aussi peu à peu familière grâce aux progrès des ordinateurs et à leur utilisation dans la vie courante. Ceux-ci deviennent chaque jour plus compacts et plus puissants de sorte qu’on peut se demander jusqu’où le progrès technique peut aller.

Un des problèmes rencontrés par les ingénieurs est le dégagement de chaleur. Je revois encore la machine IBM 650 de l’observatoire de Meudon que j’ai utilisée pour mon travail de thèse au début des années 60. Comparable en plus lent à ce qu’on appelle de nos jours une calculette programmable, cette énorme machine à lampe dégageait une telle chaleur qu’une demi douzaine de climatiseurs étaient nécessaires pour refroidir la grande salle qui la contenait. Bien que beaucoup plus faible, la chaleur dégagée par les circuits intégrés modernes reste suffisante pour empêcher la fabrication de circuits compacts à trois dimensions. La question s’est donc posée de savoir s’il existe une limite inférieure fondamentale à la dissipation d’énergie d’un ordinateur.

Les opérations effectuées par les ordinateurs peuvent toutes se décomposer en opérations logiques élémentaires faisant partie de ce que les mathématiciens appellent l’algèbre de Boole, du nom du logicien britannique George Boole. Elles s’appliquent à des variables dites booléennes pouvant prendre seulement deux valeurs 0 ou 1. Certaines de ces opérations sont réversibles. Par exemple la négation est une opération réversible notée NON (ou NOT). Elle remplace la valeur 0 par 1 et la valeur 1 par 0. D’autres opérations booléennes sont irréversibles, par exemple l’opération ET (ou AND). Appliquée à deux variables booléennes, cette opération donne pour résultat 1 si et seulement si les deux variables sont égales à 1. Le résultat 0 pouvant être obtenu de plusieurs façons différentes, cette opération est clairement irréversible.

Dans un ordinateur les opérations booléennes sont effectuées par des systèmes physiques. Si l’opération est réversible, elle pourra être effectuée par un système subissant une transformation réversible. On a vu (article 7) qu’une telle transformation idéale se fait sans dégagement de chaleur. Par contre une opération irréversible sera en général effectuée par un système physique dissipatif, c’est-à-dire dégageant de la chaleur.

Des chercheurs comme Edward Fredkin ont montré qu’il est possible de développer une logique dite “conservative” dans laquelle toutes les opérations logiques sont réversibles, sauf l’effacement du contenu d’une mémoire qui reste évidemment irréversible. L’inconvénient de la logique conservative est de produire des résultats supplémentaires non désirés appelés “déchets numériques”. Ces résultats encombrent la mémoire de l’ordinateur et ne peuvent être effacés sans dissipation d’énergie. Une solution à ce problème est de sauver les résultats désirés et d’inverser le calcul puisque celui-ci est réversible. Les déchets numériques sont alors “recyclés”. L’ordinateur se retrouve dans l’état initial prêt à effectuer de nouveaux calculs. C’est l’équivalent informatique du cycle de Carnot, le cycle réversible du moteur thermique idéal.

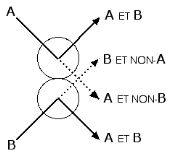
Inversement, un ensemble de particules en interaction, comme celles d’un gaz dans un moteur thermique, peut être considéré comme un ordinateur effectuant des opérations logiques. Pour le montrer, Fredkin a développé un modèle théorique dit de “boules de billard”. Dans ce modèle idéal, les boules de billard se déplacent sans frottement et les chocs sont purement élastiques. Les trajectoires sont alors parfaitement réversibles. La figure ci-dessous montre que le choc de deux boules de billard est effectivement l’équivalent d’une opération logique réversible. On observe les boules A et B sur les trajectoires en trait plein si et seulement si elles sont toutes deux présentes. On ne les observe sur les trajectoires en pointillé que si l’une d’entre elle est présente. On remarque l’abondance de résultats non-nécessairement désirés (déchets numériques).

Choc entre deux particules considéré comme une opération logique

Mais l’univers n’est-il pas un ensemble de particules en interaction? Dans ce cas l’univers est, comme le pense Fredkin, un immense ordinateur. Mais que calcule-t-il? Le lecteur assidu de ce blog aura sans doute deviné la réponse. L’univers suit un algorithme d’optimisation. Il cherche constamment à maximiser la dissipation d’énergie (ou taux de production d’entropie).

Dans le cas d’un système isolé, la solution est triviale. L’algorithme répartit également l’énergie entre toutes les particules ou, plus généralement, entre tous les degrés de liberté du système. Les variations de température, de pression ou de toute autre variable macroscopique s’estompent. Intégralement convertie en chaleur, l’énergie libre disparait. Le système tend vers ce qu’on appelle l’équilibre thermodynamique.

Si, par contre, le système est soumis à des différences de température, de pression ou de concentration chimique, et que ces différences ou gradients sont maintenus par un apport constant d’énergie, alors la solution est loin d’être triviale. Apparaît ce que nous avons appelé des structures dissipatives auto-organisées. Le système cherche toujours à atteindre l’équilibre thermodynamique mais sa trajectoire dans l’espace des phases (article 24) est limitée par la contrainte ainsi imposée. Elle reste confinée dans un volume restreint.

Dans le cas d’un gaz soumis à un certain gradient de pression ou de température, on voit apparaître des mouvements cycliques (articles 10 et 11). Lorsqu’on augmente le gradient, des mouvements de fréquence plus élevée apparaissent. C’est l’évolution vers le chaos décrite à l’article 20. Dans l’espace des phases, la trajectoire du système est d’abord périodique comme un son simple devenant de plus en plus riche en harmoniques. Au stade du chaos, la trajectoire n’est plus périodique. Elle remplit peu à peu l’espace restreint disponible sans jamais passer deux fois par le même point. Prédit en 1971 par un physicien mathématicien David Ruelle, ce phénomène baptisé “attracteur étrange” avait été découvert empiriquement dès 1963 par un météorologue, Edward Lorenz à partir de simulations numériques. David Ruelle ignorait cette découverte publiée dans une revue de météorologie. En 1976, un astronome français Michel Hénon en publiait un autre exemple l’attracteur de Hénon.

Les interactions entres molécules ne se limitent pas aux chocs. Des réactions chimiques peuvent se produire. En présence d’un fort gradient de concentration, des cycles chimiques peuvent apparaitre et s’auto-entretenir. Nous avons vu que la vie est apparue ainsi. Il n’est donc pas étonnant de retrouver des phénomènes similaires dans la reproduction des êtres vivants (suite logistique de l’article 20). Quelques années plus tard un autre physicien théoricien Mitchell Feigenbaum montrait effectivement l’universalité de cette évolution vers le chaos. Nous serions ainsi nous-mêmes des attracteurs étranges. Confinés dans l’espace, nous restons semblables à nous mêmes mais jamais parfaitement identiques. Notre cheminement est imprévisible.

Liens internet:
http://www.columbia.edu/acis/history/650.html
http://fr.wikipedia.org/wiki/Algèbre_de_Boole_(logique)
http://fr.wikipedia.org/wiki/George_Boole
http://en.wikipedia.org/wiki/Edward_Fredkin
http://fr.wikipedia.org/wiki/Cycle_de_Carnot
http://fr.wikipedia.org/wiki/David_Ruelle
http://fr.wikipedia.org/wiki/Attracteur_Étrange
http://fr.wikipedia.org/wiki/Edward_Lorenz
http://fr.wikipedia.org/wiki/Attracteur_de_Hénon
http://fr.wikipedia.org/wiki/Mitchell_Feigenbaum

La logique conservative est décrite dans un article en anglais de Fredkin et Toffoli disponible sur l’internet: http://www.cs.princeton.edu/courses/archive/fall05/frs119/papers/fredkin_toffoli82.pdf