Chers lecteurs,
J’ai arrêté ce blog fin 2007. Plusieurs d’entre vous m’ont fait part de leur déception. Je l’ai fait pour me consacrer à la rédaction de deux livres sur des sujets traités en grande partie dans ce blog.
Le premier livre, écrit en français, est destiné à un très large public. Il devrait paraître cette année aux éditions Paroles. Son titre: “Le pain, le levain et les gènes”. J’y prends comme exemple la nourriture pour expliquer ce qu’est l’évolution. Le second, rédigé en anglais, est un ouvrage pluridisciplinaire s’adressant aux scientifiques: physiciens, biologistes, économistes et historiens. Son titre: “Thermodynamics of evolution”. Sa rédaction me prendra plus de temps. Je signalerai ici leur parution.
En attendant, vous trouverez ci-dessous un court texte, à caractère politique dans lequel je reprends plusieurs thèmes développés dans ce blog.
Bonne lecture.
L’homme, la vie
et la dissipation d’énergie
François Roddier
Janvier 2009
Une nouvelle loi fondamentale de la physique a été récemment découverte. Il s’agit d’un théorème abstrait de mécanique statistique dont la démonstration a été publiée en janvier 2003, dans le plus grand journal européen de physique mathématique (J. of Physics A). Personne n’en a parlé dans les journaux. Peu de gens en ont encore vraiment saisi l’importance.
La démonstration est due à un chercheur d’origine écossaise Roderick Dewar, travaillant à Bordeaux à l’INRA. Pourquoi l’INRA? Parce que ce théorème a des implications fondamentales en biologie. Il s’applique en particulier à l’homme et à l’évolution des sociétés humaines.
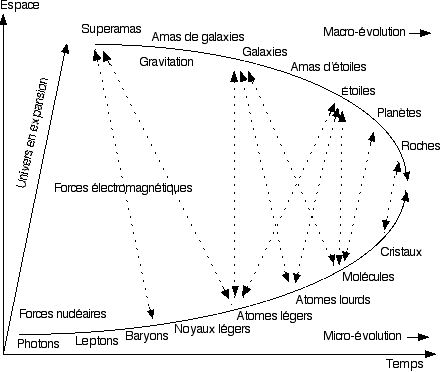
Il implique que, depuis sa création, l’univers évolue en formant des structures matérielles de plus en plus complexes capables de dissiper de plus en plus efficacement l’énergie. Les étoiles, les planètes, les plantes, les animaux, et enfin l’homme forment une telle suite de structures.
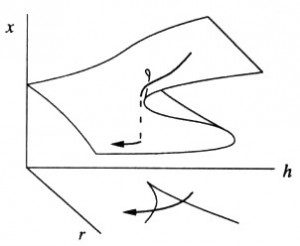
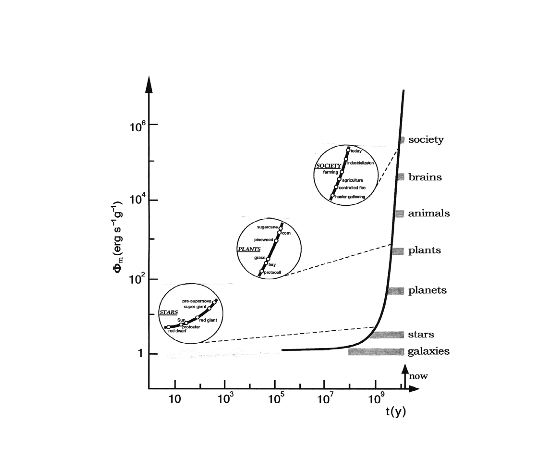
En physique, la puissance dissipée s’exprime en watts. L’efficacité avec laquelle une structure matérielle dissipe l’énergie peut s’exprimer en watts par kilogramme de matière. L’astronome américain Eric Chaisson a tracé une courbe montrant l’efficacité avec laquelle les structures citées plus haut dissipent l’énergie en fonction de l’âge de l’univers. Cette courbe est reproduite à la fin de ce texte. La progression est foudroyante.
Pour un physicien, la vie est apparue sur Terre pour dissiper l’énergie solaire. Dès 1905, Ludwig Boltzmann, père de la mécanique statistique et grand admirateur de Darwin, écrivait: “la vie est une lutte pour l’énergie libre” (c’est-à-dire l’énergie qui peut être dissipée).
Dès 1922, le chercheur américain Alfred Lotka écrivait: “la sélection naturelle tend à maximiser le flux d’énergie à travers une structure organique”. Un peu plus tard, il ajoute: “le principe de sélection naturelle agit comme si c’était une troisième loi de la thermodynamique” (c’est-à-dire une nouvelle loi de la mécanique statistique).
Cette loi est maintenant démontrée. C’est la loi de Dewar. Comme l’évolution de l’univers, l’évolution des espèces est un processus de maximisation du taux de dissipation de l’énergie. L’évolution de l’humanité n’y échappe pas. La physique et la biologie nous montrent comment ce processus fonctionne.
C’est un chercheur belge, d’origine russe, Ilya Prigogine qui a étudié le premier ce processus en détail. Son travail lui a valu le prix Nobel en 1977. Les étoiles, les planètes, les plantes, les animaux, l’homme, les sociétés humaines sont des structures dissipatives au sens de Prigogine.
En mécanique statistique, la dissipation d’énergie porte le nom de “production d’entropie”. La loi de Dewar s’appelle “MEP” (en anglais: maximum entropy production). Une structure dissipative a la propriété de s’auto-organiser. Ce faisant, elle diminue son entropie interne en l’exportant à l’extérieur. Elle maximise le flux d’entropie vers l’extérieur.
Depuis les travaux du chercheur américain Claude Shannon (1948), on sait qu’entropie et information sont deux aspects opposés d’un même concept. En exportant de l’entropie, une structure dissipative importe de l’information venant de son environnement. Elle mémorise cette information.
Chez les plantes ou les animaux, l’information sur l’environnement est principalement mémorisée dans les gènes. Plantes et animaux sont adaptés à un environnement particulier. Cette adaptation se fait par sélection naturelle. Sont sélectionnés, les plantes où les animaux qui se reproduisent le plus vite, c’est-à-dire ceux qui accroissent le plus rapidement la dissipation d’énergie.
En dissipant l’énergie, un être vivant modifie son environnement. Ses ressources naturelles s’épuisent ou se modifient. Les proies dont il se nourrit évoluent pour échapper à leurs prédateurs. Dès que l’environnement change, les gènes doivent évoluer à leur tour.
Tout être vivant est ainsi pris dans un cycle infernal que le biologiste Leigh van Vallen a baptisé “l’effet de la reine rouge”, en référence au livre de Lewis Carrol “Alice à travers le miroir” dans lequel la reine rouge dit: “ici, il faut courir le plus vite possible pour rester sur place”.
Pour rester en harmonie avec un environnement qu’il fait évoluer, un être vivant doit évoluer toujours plus vite. C’est la raison pour laquelle la dissipation d’énergie croit de plus en plus rapidement. L’information mémorisée dans les gènes ne cesse d’augmenter. Les êtres vivants deviennent de plus en plus complexes.
Beaucoup de biologistes pensaient que l’adaptation à l’environnement se faisait de façon progressive. En 1972, le paléontologue américain Stephen Jay Gould montre que ce n’est pas le cas. Quasi-stationnaires pendant de plus ou moins longues périodes les espèces vivantes tendent à disparaître de façon brutale, laissant la place à de nouvelles espèces. C’est le phénomène des équilibres ponctués.
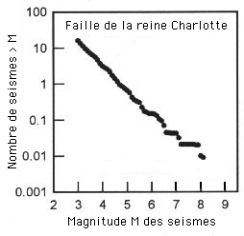
En 1993, le physicien danois Per Bak et son collègue Kim Sneppen montrent que ce phénomène est une conséquence de la façon dont l’énergie se dissipe dans l’univers, un processus physique baptisé “SOC” (en anglais: self-organized criticallity). Dewar montrera ensuite que le phénomène “SOC” est une conséquence de la loi “MEP”. Le phénomène “SOC” fait que de nouvelles espèces animales apparaissent assez fréquemment, de nouveaux genres plus rarement, de nouvelles familles exceptionnellement.
La famille des hominidés est apparue il y a environ 7 millions d’années à la suite d’un changement climatique en Afrique orientale. La savane ayant remplacé la forêt, la population de primates s’est effondrée. N’ayant plus de fruits à manger, quelques rares individus ont réussi à survivre en mangeant des racines qu’ils pouvaient arracher de leurs mains. Il leur fallu quelques dizaines de milliers d’années pour s’adapter à cette nouvelle nourriture. Ce furent les premiers hominidés, d’un genre baptisé “australopithèque”. Ils se diversifièrent en de nombreuses espèces.
Il y a environ 2,5 millions d’années, un nouveau changement important de l’environnement a donné naissance au genre “homo”. Pour survivre, le premièr représentant de ce genre, l’homo abilis, a dû manger des restes d’animaux tués par d’autres espèces animales. Ses gènes ont mis à nouveau plusieurs dizaines de milliers d’années pour s’adapter à cette nouvelle nourriture.
Il sera bientôt suivi d’une floraison d’espèces homo sachant toutes capturer et tuer leur propre gibier. Quittant l’Afrique le genre homo se répand dans le monde à la poursuite de nourriture et se multiplie. Ayant appris à se couvrir de peaux de bêtes et à domestiquer le feu, l’homo erectus affronte le froid des pays nordiques.
C’est l’époque de la disparition des grands mammifères. Ayant vraisemblablement épuisé leur environnement, les diverses espèces homo s’éteignent les unes après les autres. A la fin du paléolithique, il n’en reste plus qu’une: l’espèce homo sapiens. Un phénomène nouveau, absolument unique dans l’évolution, va alors se produire.
Cela se passe il y a dix mille ans au moyen orient. En quelques siècles seulement, l’espèce homo va changer totalement de nourriture, sans évolution notable de ses gènes. L’homme se met à manger des céréales, une nourriture à laquelle son système digestif est totalement inadapté. Comment a-t-il fait?
Il a découvert la cuisson des aliments. Le même phénomène va bientôt se reproduire de façon indépendante en Chine, puis en Amérique du sud et finalement en Amérique du nord. C’est ce qu’on appelle la révolution néolithique. Apparaissent alors l’agriculture et l’élevage. Ces nouvelles techniques se répandent comme des traînées de poudre.
La sélection naturelle, qui favorisait jusqu’ici les gènes dissipants le plus d’énergie, favorise maintenant les techniques ou cultures (dans tous les sens du terme), permettant une adaptation beaucoup plus rapide à l’environnement. L’information sur l’environnement qui était jusqu’ici mémorisée principalement dans les gènes et maintenant aussi mémorisée dans le cerveau de l’homme.
L’américain Ray Kurzweil estime la capacité du cerveau humain à environ 10 Gigabits comparé à 1 Gigabit pour les gènes. A partir du néolithique, le cerveau va contrôler l’évolution de l’humanité. Le zoologiste anglais Richard Dawkins a proposé d’appeler “mèmes” les éléments d’information enregistrés dans le cerveau par analogie avec les “gènes”. Chez l’homme, les mèmes ont remplacé les gènes. Les conséquences en sont considérables.
Alors que les gènes se reproduisent lentement par transmission génétique, les mèmes se transmettent à toute vitesse grâce au langage. Un nouveau type de structures dissipatives s’auto-organise formé d’individus partageant les mêmes connaissances ou “mèmes”. Ce sont les premières sociétés humaines. Tandis que les gènes n’évoluent plus ou évoluent trop lentement, ce sont maintenant les “mèmes” qui évoluent et se diversifient. La sélection naturelle va désormais favoriser les mèmes les plus dissipatifs d’énergie. La sélection naturelle agit désormais sur les sociétés.
Apparaît une nouvelle forme de mémorisation de l’information propre à ces sociétés: l’écriture. On sait que l’écriture est apparue pour comptabiliser les échanges. Elle est secondée par l’invention de la monnaie, fondement de l’économie. Le développement de l’économie n’est rien d’autre que le développement de la dissipation d’énergie par les structure dissipatives que sont les sociétés humaines. Avec la monnaie, celle-ci fait un grand bon en avant.
Peu d’économistes ont réalisé que l’économie est une branche de la mécanique statistique. Robert Ayres et Nicolas Georgescu-Roegen ont sans doute été les premiers vers 1970. Malheureusement, ils se réfèrent essentiellement à la thermodynamique du 19ème siècle qui ne s’applique qu’au voisinage de l’équilibre. Elle ne s’applique pas à l’économie qui est un processus dissipatif entièrement hors équilibre.
Il ne fait aucun doute que les résultats de Dewar et de Per Bak deviendront un jour les piliers d’une nouvelle science économique, lorsque les économistes voudront bien s’apercevoir de leurs travaux. Les plus avancés d’entre eux découvrent seulement maintenant l’importance primordiale de l’information en économie. L’histoire montre que l’évolution favorise toujours les sociétés qui dissipent le plus d’énergie, c’est-à-dire celles qui ont le développement économique le plus rapide.
Dans une société les individus sont soumis à des contraintes qui limitent leur liberté. Plus une société est organisée, plus ces contraintes sont fortes. Comme a dit Rousseau: “l’homme est né libre, et partout il est dans les fers”. Ces contraintes ne sont pas nécessairement optimisées pour maximiser la dissipation d’énergie. L’évolution va donc tendre à les éliminer pour les remplacer par des contraintes mieux optimisées. C’est l’auto-organisation de la société. Son mécanisme est la sélection naturelle. Chez l’homme, elle agit essentiellement sur les “mèmes” (évolution culturelle) non seulement au niveau des individus, mais aussi au niveau des sociétés (sélection de groupe).
Les “mèmes” ayant remplacé les gènes, une société d’individus partageant les mêmes “mèmes” devient en soi une espèce mémétique. Aucune espèce animale n’attaque sa propre espèce. Une espèce qui le ferait mettrait ses gènes en danger. Elle serait vite éliminée par la sélection naturelle et remplacée par une espèce concurrente. Devenue unique, l’espèce homo sapiens n’a plus aucune concurrence.
Un membre d’une espèce mémétique peut alors domestiquer un membre d’une autre espèce mémétique, comme on domestique un animal. Il en fait un esclave. Il peut aussi tuer un membre d’une autre espèce mémétique sans mettre en danger sa propre espèce. C’est l’extermination des peuples primitifs par les envahisseurs blancs.
Avec la découverte des énergies fossiles, une nouvelle révolution arrive, la révolution industrielle. A la pointe de l’industrialisation, l’Angleterre est le premier pays à limiter les pouvoirs de sa monarchie. La révolution française suit. Parce que la monarchie entravait le développement de l’économie, elle était condamnée à disparaître.
Au vingtième siècle deux idéologies s’affrontent, le capitalisme et le communisme. Ce sont des espèces mémétiques différentes. Le communisme finit par succomber parce qu’il ne permettait pas une dissipation aussi efficace de l’énergie. Le libéralisme envahit le monde comme un feu de forêt. Cela a plusieurs effets.
La concurrence dite libre et non faussée, donne libre cours à la sélection naturelle entraînant une croissance sans bornes des inégalités entre les nations (sélection de groupe) et entre les individus d’une même nation (sélection individuelle). Ces inégalités favorisent à leur tour la dissipation d’énergie.
En augmentant la dissipation d’énergie, le libéralisme accélère l’évolution, ce qui déstabilise les sociétés. Celles-ci doivent en effet sans cesse s’adapter, se réorganiser. C’est l’effet de la reine rouge de van Vallen. Or la vitesse à laquelle une société ou espèce mémétique évolue est limitée par la vitesse à laquelle les mèmes sont transmis d’une génération à une autre. C’est l’effondrement du système scolaire, signe précurseur de l’effondrement d’une société.
Plus une société dissipe d’énergie, plus elle modifie son environnement physique. Une conséquence de la révolution industrielle est le réchauffement climatique. Tout ceci n’est pas nouveau. Les sumériens ont transformé en désert les terres fertiles du moyen orient. La majorité des grandes civilisations du passé se sont effondrées de la même façon. C’est le processus “SOC” du physicien Per Bak. Le même phénomène se produit actuellement à l’échelle de la planète.
On comprend maintenant la fatalité de l’histoire. Le même processus se répète sans cesse, chaque fois sous une forme différente. C’est le processus général de dissipation de l’énergie dans l’univers. La cause de tous nos maux est enfin élucidée. Pour y remédier, il suffirait de limiter notre dissipation d’énergie. Mais est-ce faisable?
Le problème est celui de l’irréversibilité thermodynamique. La sélection naturelle est un processus irréversible. Si, pour le bien commun, un individu décide de limiter sa dissipation d’énergie, alors il sera tôt ou tard éliminé dans la compétition avec les autres. La réversibilité n’est possible que si tous les individus de notre planète décident solidairement de diminuer leur dissipation d’énergie. Il suffit alors qu’un seul individu refuse de coopérer pour qu’il reprenne l’avantage, auquel cas toute la coopération s’effondre.
La situation apparaît sans espoir. Elle l’est moins à l’échelle des nations. Nombre d’entre elles ont signé les accords de Kyoto. Hélas, il suffit que l’une d’entre elles refuse (les États-Unis) pour annihiler le résultat. Les habitants de la planète n’accepteront de limiter leur dissipation d’énergie que s’ils sont tous convaincus d’en tirer avantage et si chacun est confiant que tous les autres en feront autant.
Un aspect du problème est que la relation explicitée ici entre la dissipation de l’énergie et le bonheur individuel est difficile à saisir. Le principe de libéralisation de l’économie paraît à priori séduisant. Le mot libéralisme a la même racine que le mot liberté. Il libère en effet l’individu des contraintes arbitraires. Il a conduit jusqu’ici l’humanité vers plus de démocratie. Mais surtout le libéralisme favorise la croissance qui est synonyme de paix, de progrès et de prospérité.
Pour la majorité des économistes, favoriser la croissance est le postulat de base de toute économie. La déclaration d’indépendance américaine reconnaît à chacun un droit inaliénable à la vie, à la liberté, et à la recherche le bonheur (pursuit of happiness). Le libéralisme semble apporter une bonne réponse à ce besoin. Mais c’est une réponse à court terme.
Un bonheur à long terme n’est possible qu’en harmonie avec l’environnement. Hélas, au lieu de tendre vers l’harmonie en restant au voisinage de l’équilibre thermodynamique, le libéralisme maximise la dissipation d’énergie en maximisant le déséquilibre thermodynamique. Étant le plus efficace à dissiper l’énergie, il est aussi le plus efficace à épuiser les ressources et à polluer l’environnement. Il oblige l’homme à évoluer toujours plus vite.
Pour faire face à l’épuisement des ressources et à la pollution, la société doit sans cesse évoluer. Elle le fait en imposant constamment à l’homme de nouvelles contraintes. Ainsi, au lieu de libérer l’individu, le libéralisme l’asservit davantage. En favorisant la sélection naturelle, il accroît les inégalités. Le résultat est moins de liberté, moins d’égalité, moins de fraternité. Il s’oppose aux valeurs de notre République.
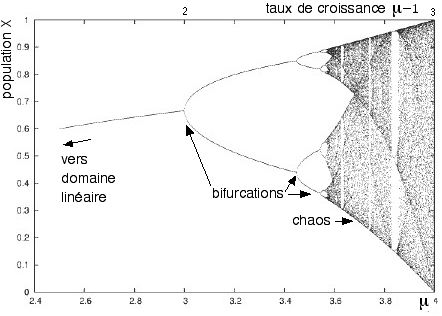
Doit-on pour autant renoncer à la croissance et au progrès? A moins de faire preuve d’ascétisme, cela paraît difficile, mais on peut tenter d’en rendre les contraintes acceptables. Elles le deviennent dans la mesure où nous avons le temps de nous y adapter. Pour cela, l’évolution doit être suffisamment lente. Comme nous l’avons vu, la société ne doit pas changer de façon notable entre deux générations. Il suffirait donc de limiter notre taux de dissipation de l’énergie en conséquence. En termes de mécanique statistique cela veut dire rester dans le domaine linéaire des transformations quasi-réversibles d’Onsager. Certains appellent cela le développement durable.
Le phénomène de production maximale d’entropie n’est qu’une propriété statistique valable pour un nombre suffisant d’éléments. Si notre planète se réduit à une société unique d’individus solidaires, il ne s’applique plus. Dans son ensemble, l’humanité reste maîtresse de sa destinée. Le seul espoir est donc une prise de conscience à l’échelle internationale.
Une telle prise de conscience semble prendre effectivement naissance grâce au fait que pour la première fois la dégradation de l’environnement devient visible dans le temps d’une génération, signe d’un nouveau séisme à l’échelle mondiale. Le coût d’une nouvelle restructuration de la société commence à paraître prohibitif non pas sur le plan humain mais sur le plan économique. D’où un appel effectif pour un développement durable. En essayant de sauver la planète (qui s’en moque), nous sauverons peut-être l’homme.
|
|
Évolution du taux de dissipation de l’énergie (par unité de masse) en fonction de l’âge de l’univers (d’après Eric Chaisson) |